와사비 종류
혼와사비(일본 토착 와사비)
혼와사비 또는 일본 토종 와사비는 심는 방법에 따라 더욱 분류할 수 있다:하천에 심으면 사와사비, 밭에 심으면 하타케와사비라고 한다.
사와 와사비
일본 고유의 야생식물인 와사비는 브라시카과 또는 겨자과에 속하는 상록수 초본 다년생이다. 사와사비는 깊은 산지의 계곡과 고랑을 흐르는 차고 맑은 물에서 야생으로 자라며 비슷한 조건을 가진 곳에서 재배한다. 최적의 재배 장소는 여름철 16℃, 겨울에는 10℃의 온도를 유지하는 풍부한 샘물이 있는 곳으로 낙엽수 숲으로 둘러싸여 있고, 여름에는 나무 덮개로 그늘을 드리우고, 나무 사이를 통과하는 따뜻한 햇살을 받을 수 있을 것이다. 시즈오카 현 이즈 구에는 앞에서 언급한 혼와사비 재배에 최적의 조건을 제공하는 계곡과 협곡이 있다. 따라서 일본 최대의 혼와사비 생산지역은 이즈(李州)에 있다.
하타케와사비
단순히 흙에 씨앗을 뿌려서 자라는 와사비는 그래서 하타케와사비 "하타케"는 "밭"을 의미한다. 주로 줄기 수확을 목적으로 재배되며, 도쿄는 물론 시즈오카, 나가노, 시마네, 야마구치 현 등지의 강제 재배(온실을 사용)에 의해 재배된다. 또한 대만, 인도네시아, 캐나다와 같은 나라에서도 해외에서 재배되고 있다. 이 중 대다수는 와사비스케(채취한 와사비)와 와사비 페이스트 등 가공제품에 쓰인다.
세요와사비
세요와사비는 북유럽에서 재배되는 다년생 식물이다. 일본에서는 와사비다이콘(다이콘 = 일본백무)이라고도 한다. 영어로는 고추냉이, 프랑스어로는 라이포트라고 한다. 혼와사비와 비슷한 매운 맛을 내기 때문에 향신료로 많이 쓰인다. 뿌리부분도 얇게 썰어 고기요리의 고명으로 쓰거나 생선요리를 드레싱하기 위한 소스로 갈아서 사용한다. 중세 이후 유럽에서도 약용으로, 방부제로, 또는 식욕을 돋우기 위해 사용되어 왔다. 오늘날에는 말려서 가루와사비의 주재료로 쓰인다.
Life Hacking
- 와사비 종류 2020.04.28
- [Pandas] read_csv 시 UnicodeDecode 에러 : utf-8 인코딩 문제 2020.04.23
- [EfficientDet] 논문 리뷰: 가볍지만 성능은 좋은 object detector 2020.04.09
- [EfficientNet] 논문 리뷰: 모델의 파라미터(스케일링)에 대한 고찰 2020.04.09
- [Multiple Comparisons & Adjustment] Adjusted P-value란? ( Bonferroni, Holm, Hommel, BH, BY) 2020.04.02
- [GNN] (1) 데이터 구조 분석을 위한 Graph Neural Network(GNN) 소개 2020.03.25
- [SimPy] 파이썬 시뮬레이션: 기초 알아보기 2020.03.16
- Contrast set learning & treatment learning (STUCCO, TAR3) 2020.01.28
- [LightGBM] LGBM는 어떻게 사용할까? (설치,파라미터튜닝) 2020.01.27
- [Math] 범함수와 최적제어 변분법의 관계 2019.04.14
와사비 종류
[Pandas] read_csv 시 UnicodeDecode 에러 : utf-8 인코딩 문제
[Pandas] UnicodeDecode 에러 : utf-8 인코딩 문제
판다스로 read_csv를 사용해서 csv 파일을 읽을 때, 특정 문자열 때문에 에러가 발생하는 경우가 있다.

UnicodeDecodeError: 'utf-8' codec can't decode byte 0xa1 in position 22: invalid start byte
이 에러를 해결하는 방법은 encoding='CP949'을 아래와 같이 추가해주는 것이다.
df = pd.read_csv("xxx.csv", encoding='CP949')
'Statictics & Math & Data Science > 파이썬 데이터 분석' 카테고리의 다른 글
| [LightGBM] LGBM는 어떻게 사용할까? (설치,파라미터튜닝) (0) | 2020.01.27 |
|---|---|
| [Regression] Ridge and Lasso Regression in Python (3) - Lasso (0) | 2019.01.31 |
| [Regression] Ridge and Lasso Regression in Python (2) - Ridge (0) | 2019.01.31 |
| [Regression] Ridge and Lasso Regression in Python (1) - Polynomial (0) | 2019.01.31 |
| [Regression] Piecewise Regression with numpy (0) | 2019.01.29 |
[EfficientDet] 논문 리뷰: 가볍지만 성능은 좋은 object detector
EfficientNet과 마찬가지로 EfficientDet은 모델 사이즈를 최소화하고 성능을 최대화하는 효율성에 초점을 맞춘 object detection 모델이다. 이 논문은 EfficientNet을 backbone 네트워크로 사용하였고 bi-directional feature pyramid network (BiFPN)을 이용하여 특징을 쉽고 빠르게 융합하는 방식을 제안하였다. 기존의 object detector는 region-of-interest proposal 단계를 가지는지 여부에 따라 two-stage 방식과 one-stage 방식으로 구분되었다. Two-stage detector가 더 정확하고 유연한 반면, one-stage detector는 사전에 정의된 anchor를 이용하여 간단하며 효과적인 방식으로 detection을 수행한다. Object detection에서 어려운 점 중에 하나는 상황에 따라 object의 크기가 달라지는 것을 고려해야 한다는 점이다. 따라서 멀티-스케일링 기법이 중요하며, feature pyramid network (FPN)을 시작으로 multi-scale feature를 합치는 방법이 연구되고 있다. M2det은 특징 합성을 위한 U-shape 모듈을 사용하였고, G-FRNet은 특징 정보를 컨트롤하기 위한 gate units을 도입하였다. 더 나은 성능을 얻기 위해, 베이스라인 detector의 스케일을 키우는 방식을 많이 사용하며 backbone 네트워크로 ResNet, ResNeXt, AmoebaNet을 사용하기도 한다.
아래의 그림은 EfficientDet의 전체적인 구조로, 전체적으로 one-stage detector의 패러다임을 따르고 있다. Backbone 네트워크인 EfficientNet의 level 3-7 features {P3, P4,P5,P6,P7} 를 추출하여 top-down과 bottom-up 양방향으로 특징 융합을 수행한다. 융합된 특징은 class/box 예측 네트워크로 전달되어 객체의 클래스와 바운딩 박스를 예측한다.

정확도와 효율성의 trade off를 최적화하는 baseline 모델을 선택하는 것은 매우 중요하다. 기존 연구는 ResNeXt와 AmoebaNet를 기반으로 큰 이미지를 대상으로 했다. 이러한 방법은 하나의 스케일링 차원에만 집중하기 때문에 효율적이지 못하다. 이러한 문제를 해결하기 위해. EfficientDet은 EfficientNet과 마찬가지로 효율적인 compound scaling 방식을 사용하였다. BiFPN을 구성할 때, 채널의 수는 지수적으로 증가시키고 레이어의 수는 선형적으로 증가시켰다.
Wbifpn=64∙1.35∅, Dbifpn=2+∅
Feature level이 3-7인 layer는 BiFPN이 사용되므로, 입력 이미지의 해상도를 27 로 나눠야 하며 해상도를 선형적으로 증가시키기위해 다음과 같음 방식으로 해상도를 결정하였다.
Rinput=512+∅∙128
Object의 location과 class를 예측하는 네트워크도 compound coefficient를 사용한다. 그 중 너비(width)는 BiFPN과 동일하고 (Wpred=Wbifpn ), 레이어 수는 다음과 같은 방식으로 결정한다.
Dbox=Dclass=3+∅∙128
위의 식에서 compound coefficient ∅ 에 따라 EfficientDet-D0(∅=0 ) 부터 D6(∅=6) 까지 정리한 결과는 다음의 표와 같다.

아래의 표에서 #Params와 #FLOPS는 모델 파라미터와 연산의 수를 나타낸다. LAT는 배치 크기가 1일때의 의 추론 지연 시간을 나타내고, AA는 autoaugmentation 을 의미한다. EfficientDet은 mAP 성능이 유사한 object detection 모델과 비교하여 파라미터 수와 필요 연산량이 훨씬 적은 것을 확인할 수 있다. 따라서, 추론 속도도 동일 성능의 다른 모델에 비해 2배 가량 빠르다.

결론적으로, EfficientDet은 복합 스케일링 (compound scaling) 기법을 이용하여 효율적으로 성능을 향상시키고 #Params와 #FLOPS를 줄였다. Object detection 모델을 이용한 좌표 보정 알고리즘에서도 EfficientDet을 사용하여 부품의 위치와 레이블을 추론함으로써, 기존 detector 보다 정확도와 처리속도를 향상시킬 수 있었다.

[참조] TAN, Mingxing; PANG, Ruoming; LE, Quoc V, “Efficientdet: Scalable and efficient object detection.” arXiv preprint arXiv:1911.09070, 2019.
'Statictics & Math & Data Science > Neural Networks' 카테고리의 다른 글
| [EfficientNet] 논문 리뷰: 모델의 파라미터(스케일링)에 대한 고찰 (0) | 2020.04.09 |
|---|---|
| [GNN] (1) 데이터 구조 분석을 위한 Graph Neural Network(GNN) 소개 (0) | 2020.03.25 |
[EfficientNet] 논문 리뷰: 모델의 파라미터(스케일링)에 대한 고찰
EfficientNet 논문은 ConvNets의 스케일을 높이는 기존 접근법을 다시 한번 짚고 넘어가자는 의미의 ‘Rethinking’을 논문의 타이틀로 사용하였다. 이 논문은 기존 ConvNets들이 성능을 향상시키기 위해 사용한 방법들을 구분하여 소개하고, 성능을 향상시키면서 모델 연산량을 최대화하는 효율적인 ConvNets을 제안한다.
2012년 AlexNet (Krizhevsky et al., 2012)을 시작으로 ImageNet 대회에서 정확도는 큰 폭으로 향상되었다. GoogleNet (Szegedy et al., 2015)는 6.8M의 파라미터 수를 가진 모델로 74.8%의 top-1 accuracy를 달성했으며, SENet (Hu et al., 2018)은 145M의 파라미터 수를 가진 모델로 82.7%의 top-1 accuracy를 달성했다. GPipe (Huang et al., 2019)는 557M의 파라미터 수를 가진 모델로 84.3%의 top-1 accuracy를 달성했다. 일반적으로 대부분의 어플리케이션에서는 정확도가 가장 중요하지만, 메모리의 한계도 존재하기 때문에 앞으로 높은 성능을 얻기 위해서는 효율성도 반드시 고려해야한다.
효율을 향상시킨 ConvNets은 SqueezeNet(Iandola et al., 2016; Gholami et al., 2018), MobileNets (Howard et al., 2017; Sandler et al., 2018), ShuffleNets (Zhang et al., 2018; Ma et al., 2018)이 있다. 효율적인 네트워크 구조에 대한 연구로 네트워크의 너비, 깊이, 커널 사이즈의 튜닝을 통한 효율성을 향상시킨 모델이 등장하였고, ResNet (He et al., 2016)은 네트워크의 깊이(#layer)를 조절한 ResNet-18, ResNet-200를 발표하였다. 반면, 너비(#channels)를 조절하여 스케일링한 WideResNet (Zagoruyko & Komodakis, 2016)과 MobileNets (Howard et al., 2017)은 더 큰 사이즈의 이미지를 활용하여 성능을 향상시킨 모델이다.

EfficientNet은 이러한 모델 스케일링 기법을 중점적으로 다뤄 새로운 스케일링 기법을 제안한다. 우선, 깊이(depth)를 증가시키는 방법은 많은 ConvNets에서 사용되었다. 레이어 수가 많아질수록 ConvNet은 더 다양하고 복잡한 특징을 잡아낼 수 있고, 새로운 이미지에 대한 일반화 성능도 좋아진다. 하지만 레이어 수가 많아질수록 기울기 소실 등의 문제로 학습이 어려워지는 문제가 발생한다. 너비(width)를 스케일하는 방법은 작은 사이즈의 모델에 주로 사용되며, 너비의 확장은 더욱 미세한 특징을 잡아낼 수 있고 네트워크 학습을 쉽게 만든다. 하지만, 과도한 스케일링은 고수준의 특징을 잡아내기 어렵게 하는 경향이 있다. 해상도(resolution)을 증가시키는 방법은 더욱 미세한 패턴을 잡아낼 수 있다. ConvNet의 입력 크기는 224 x 224를 시작으로 299, 331, 480 과 같이 점점 커졌고 더 높은 정확도를 보였다. Object detection ConvNets에서는 600 x 600이 가장 많이 사용된다. 해상도도 마찬가지로 해상도가 높아짐에 따라 성능 향상 폭은 감소한다.
아래의 그림은 베이스라인 모델을 각기 다른 Width(w), Depth(d), Resolution(r)를 바꿔가며 실험한 결과이다. 결과적으로 더 큰 깊이와 너비, 해상도를 가질수록 높은 성능을 달성한다. 하지만, 정확도가 80%에 도달하게 되면, FLOPS 증가에 비해 정확도 향상이 어려워진다.

일반적으로 해상도가 높아질수록 네트워크의 레이어도 많아져야 하고, 너비도 증가해야한다. 이처럼, 너비, 깊이, 해상도와 같은 스케일링 차원들은 서로 독립적이지 않으며, 균형을 잘 맞춰야 한다. 아래의 실험은 스케일링을 복합적으로 실험한 결과이다.

우선, 너비는 고정한 채로 깊이와 해상도를 변경한 경우 정확도가 빠르게 포화되는 현상을 보였다. 깊이를 증가시키고 (d=2.0) 해상도를 높인 (r=1.3) 경우, 동일한 FLOPS에서 더 높은 성능을 달성했다.
EfficientNet 논문에서는 새로운 복합 스케일링 기법을 제시하기 위해 compound coefficient ∅ 를 이용하여 스케일링 차원을 정의하였다.

α, β, γ 는 grid search를 통해 결정한 상수이고, compound coefficient ∅ 는 사용 가능한 리소스에따라 사용자가 결정하는 계수이다. 일반적인 컨볼루션 연산의 FLOPS는 d,w2, r2 에 비례한다. 예를 들어, 깊이를 증가시켜 레이어 수를 두 배로 하면, FLOPS도 두 배가 된다. 반면, 네트워크의 너비나 해상도를 두 배 증가시키면, FLOPS는 네 배 증가한다. 일반적으로 ConvNets의 연산 비용은 컨볼루션 연산이 대부분을 차지하므로 FLOPS는 (α∙β2∙γ2)^∅ 로 추정할 수 있다. 위 수식에서는 α∙β2∙γ2≈2 라는 제한조건을 설정함으로써, FLOPS를 2의 ∅ 로 추정할 수 있도록 했다.
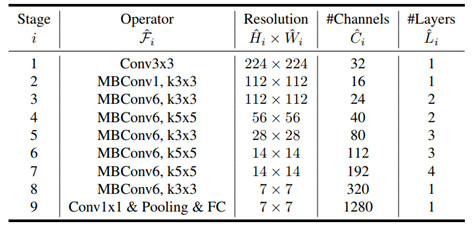
위의 표는 EfficientNet-B0의 구조이며, 주요 block은 mobile inverted bottleneck MBConv (Sandler et al., 2018; Tan et al., 2019)로 구성되어 있고 squeeze-and-excitation optimization (Hu et al., 2018)을 적용하였다. 실험은 이 베이스라인 모델로 시작하여 복합 스케일링 기법을 다음과 같이 두 단계로 적용하였다.
-
STEP 1: ∅ 를 1로 고정하고 제한 조건을 만족하는 범위 내에서 grid search로 α, β, γ 를 구한다. EfficientNEt-B0의 경우 α=1.2, β=1.1, γ=1.15 이 최적의 값이었다.
-
STEP 2: α, β, γ 를 상수로 고정하고 ∅ 를 증가시켜가며 네트워크의 스케일을 확장하고, 그 네트워크는 EfficientNet-B1부터 B7이 된다.
사이즈가 큰 모델도 마찬가지로 파라미터 최적화를 통해 스케일링 차원을 구할 수 있지만, 모델의 크기가 클수록 탐색 비용이 매우 크다. 반면, 제안된 기법은 작은 네트워크에서 α, β, γ 가 균형을 이루는 적절한 값을 찾고 compound coefficient를 증가시킴으로써 효율적인 스케일링 차원(깊이, 너비, 해상도 값) 탐색을 가능하게 한다.
결과적으로 본 논문에서 제안한 기법을 사용하여 EfficientNet-B1부터 B7을 학습시켜 ImageNet 결과를 보면, 다른 ConvNets과 비교하여 파라미터 수와 FLOPS이 훨씬 작으며 높은 성능을 보인다. 특히, EfficientNet-B7은 84.4%의 top1 / 97.1%의 top-5 accuracy를 보였으며, 66M의 파라미터 수와 37B의 FLOPS로, GPipie (Huang et at., 2018)와 비교하여 더 높은 정확도에 파라미터 수는 8.4 배 적다.

[참조] TAN, Mingxing; LE, Quoc V, “Efficientnet: Rethinking model scaling for convolutional neural networks.” arXiv preprint arXiv:1905.11946, 2019.
'Statictics & Math & Data Science > Neural Networks' 카테고리의 다른 글
| [EfficientDet] 논문 리뷰: 가볍지만 성능은 좋은 object detector (0) | 2020.04.09 |
|---|---|
| [GNN] (1) 데이터 구조 분석을 위한 Graph Neural Network(GNN) 소개 (0) | 2020.03.25 |
[Multiple Comparisons & Adjustment] Adjusted P-value란? ( Bonferroni, Holm, Hommel, BH, BY)
어떤 실험을 하고 결론을 내리기 위해선 가설 검정을 수행한 후 특정 통계량의 유의수준과 비교한다. 대게, p-value는 0.05나 0.01를 사용하곤 한다.
그러나 두 개 이상의 가설을 동시에 시험할 때(다중 비교) 통계적 추론이 잘못될 확률은 상당히 높아진다. False positive가 많이 발생하는데 생물학이나 의학에서는 이러한 거짓 양성(false positive)에 민감하여 p-value 조정(adjustment)이 필요하다. 하지만, 다양한 실험 특성에 적합한 adjustment 방법을 선택하기는 여전히 어렵다.
예를 들어 보자, Garcia-Arenzana(2014)은 스페인 여성들에게 유방암의 중요한 위험 요소인 유방조영술 밀도와 25가지 식이 변수의 연관성을 테스트했고 다음과 같은 결과를 확인했다.

보다시피 P<0.05를 만족하는 변수의 수는 5개이다. 하지만, 25개의 식이 변수를 동시에 검정했기 때문에, 식이요법이 유방조영학적 밀도에 실질적인 영향을 미치지 않았더라도, 한 두 개의 변수가 우연히 유의미한 결과를 보였을 거라고 예상했다. 이때, Bonferroni 보정을 적용하면 0.05를 25로 나눈 P<0.002를 만족해야된다. 그러면 총 칼로리(Total calories)만 유의하다.
아래에서 설명하겠지만 Bonferroni 보정의 사용은 일련의 검정에서 하나의 거짓 양성(false positive)가 문제가 될 때 적합하다. 하지만, 많은 변수를 한번에 검정해야 하고 그 중에서 의미있는 변수 여러 개를 찾고자 한다면, Bonferroni 보정은 거짓 음성(false negative)을 초래할 수 있다. 즉, 유의미한 변수를 놓칠 수 있다는 말이다.
예를 들어, 간암 조직과 정상 간 조직 사이에 있는 2만개의 유전자의 유의성을 비교한다고 하자. 당신은 의미가 서로 다른 다른 수십, 수백 개의 유전자를 찾기를 바라고 있다. 이때, Bonferroni 보정을 사용할 경우 P 값은 0.05/20000=0.0000025 보다 작아야 한다. 이렇게 되면, 단지, '단 하나의 거짓 양성도 포함하지 않는다'는 것을 확신하고자 한 이유만으로 많은 중요한 유전자 변수들을 놓칠 수 있다.
Bonferroni 교정의 중요한 문제는 통계 테스트의 "가족(family)"이 무엇인지 결정하는 것이다. 지금은 25개의 변수를 가지고 검정했는데, 여기에 연령, 교육, 사회적 지위 등과 같은 변수 13개가 추가된다면, P를 38로 나눠야 할까? 만약 이전 실험에서 다른 30개의 변수를 사용한다면 family를 55개로 정의해야 할까? 이처럼 Bonferroni adjustment에서는 family의 수를 정의하는데 어려움이 있다.
여기서 family-wise type 1 error의 개념이 나온다. family-wise type 1 error (FWER)란 family에서 false positive가 1개라도 발생할 확률을 의미한다.
FWER = 1 - Pr(V=0) = Pr(V>=1)
다중 비교 문제에 대한 고전적인 접근법은 이 FWER을 조절하는 것이다. 만약 FWER 이 0.05라면 한 연구에서 적어도 1개의 잘못된 결론이 나올 확률이 0.05라는 뜻이다. 이 FWER를 통제하기 위해 유의성 또는 알파에 대한 유의수준을 0.05로 설정하는 대신 더 낮은 임계값을 사용하는 방법이 있다.
1) Bonferroni adjustment
FWER 을 제어하는 가장 일반적인 방법은 Bonferroni 보정이다. Bonferroni adjustment는 FWER (일반적으로 0.05)을 검정 횟수로 나누어 개별 검정의 임계값(알파)을 찾는다. 만약, 100개의 통계적 시험을 수행하는 경우, 개별 검정의 임계값은 0.05/100=0.0005가 될 것이며, P<0.0005인 개별 검정은 유의하다고 간주한다.

하지만 Bonferroni 보정은 너무 보수적이어서 귀무가설이 잘 기각되지 않는 단점이 있다. 따라서 적절한 타협이 필요하다.

Multi-step 보정방법
2) Holm adjustment
Holm adjustment는 multi-step 방법 중 step-down에 해당 하는 방법이다. Bonferroni 기법을 기반으로하는 좀 덜 보수적인 방법이다. 이 방법은 가설의 유의성에 따라 정렬하는 방법을 사용하는데 그 방법은 아래와 같다.

p-value를 낮은 순으로 정렬하고 높은 rank 일수록 보수적으로 검정하는 방법이다.

3) Hochberg adjustment
Hochberg adjustment는 multi-step 방법 중 step-up에 해당 하는 방법이다. Holm method와 유사하게 Hochberg adjustment도 비슷한 방법을 사용한다.

하지만 Hochberg 방법은 p-value를 높은 순으로 정렬하고 \( p_{(i)} \leq \alpha^{'}_{(i)} \) 인 \( \textrm H_{(i)} \) 가 나오면 비교를 멈추고 유의 수준에서 귀무가설을 기각한다.
4) Hommel adjustment
Simes(1986)는 Bonferroni method를 수정하여 m개의 가설에 대해 global test를 하는 방법을 제안했다.
\( H=\{ H_{(1)}, ..., H_{(m)} \} \) 일 때, \( p_{(i)} \leq i\frac{\alpha}{m} \) 이면 귀무가설 H가 기각된다.하지만 Simes의 global test 는 개별적인 가설에 대해 접근하는 방법이 아니기 때문에 Hommel(1988)는 Simes의 방법을 확장하여 individual \( H_i \)에 대해 검정하는 방법을 제안한다.
$$ j=max \{ i \in \{ 1, ... , m \} : p_{(m-i+k)} > k{\alpha}/{i} \ for \ k=1, ... , i \}$$
만약 j 가 존재 하지 않는다면 모든 \( H_i \)는 기각되고, 존재한다면 \( H_i \)는 \( p_i \leq {\alpha}/{j} \) 를 만족하는 경우 기각한다.
5) Benjamini-Hochberg(BH) adjustment
FWER을 조절하는 방법과 달리 Benjamini와 Hochberg(1995)는 FDR(false discovery rate)을 조절하는 방법을 소개했다. FDR은 다중 비교에서 Type 1 error를 조절하는 또 다른 자주 쓰이는 지표로 유의하다고 판단한 가설 중 실제로 유의하지 않은 가설의 비율을 조절하는데 사용된다. FDR은 다음과 같이 정의한다.

여기서 m은 실험 횟수이고, \( m_0 \) 는 true(맞게 기각된) \( H_0 \) 의 수이다. R은 기각된 총 횟수, U는 잘못 기각된 \( H_0 \)의 수이다.

BH method는 아래의 방법으로 FDR 을 조절한다. q는 사전 정의된 FDR의 upper bound 이다. (e.g., q=0.05)
$$ k = max \{ i : p_{(i)} \leq \frac{i}{m}q \} $$
만약 k가 존재하지 않는다면 가설을 기각하지 못하고, 존재한다면 가설 \( H_i (i = 1, ... , k) \)를 기각한다. BH method는 p-value가 가장 큰 \( H_{(i)} \) (i=m, ..., 1) 부터 작은 순으로 비교 연산을 시작한다.
FDR 기반의 보정 방법은 다른 방법에 비해 덜 보수적이다. (Fig.1 참고) 그리고 실험 횟수가 많을 때 널리 사용된다.
아래의 그림을 보면, BH adjustment는 28개의 귀무가설을 기각하여, 보수적인 7개만 기각한 Holm's에 비해 어느정도 false positive를 허용한다.

6) Benjamini-Yekutieli (BY) adjustment
BH method와 비슷하지만 좀더 보수적인 방법이다. 마찬가지로 FDR 을 사용하여 조절하는 방법이며 Benjamini과 Yekutieli(2001)이 제안했다. 마찬가지로 q는 사전 정의된 FDR의 upper bound이다.
BY method는 아래와 같이 계산된다.

k가 존재하지 않는다면 가설을 기각하지 않고, 존재하면 가설 \( H_i \)를 기각한다.
참조: Chen, S. Y., Feng, Z., & Yi, X. (2017). A general introduction to adjustment for multiple comparisons. Journal of thoracic disease, 9(6), 1725.
'Statictics & Math & Data Science > 통계&데이터분석' 카테고리의 다른 글
| [데이터분석] 매니폴드(manifold)란? (0) | 2019.04.03 |
|---|---|
| [통계] 차원의 저주와 K-NN(최근접이웃) 알고리즘 (0) | 2019.04.03 |
| [가중치 규제] L1 & L2 Regularization Method (0) | 2019.01.30 |
| [확률분포] 확률변수, 확률질량함수, 확률밀도함수 (0) | 2018.08.15 |
| [실험계획법] 분산 분석(1) 총변동의 분할 (0) | 2018.08.10 |
[GNN] (1) 데이터 구조 분석을 위한 Graph Neural Network(GNN) 소개
그래프 구조를 가지는 데이터의 분석에 Graph Neural Network(GNN)이 언급되면서 관심을 받고 있다. 사실 그래프 이론자체가 쉽게 와닿는 내용이 아니고, 이해하기 위해 여러 자료도 봤지만 한 번에 이해를 하지 못했다. 그 중 Medium 의 블로그를 참고하여 이해한 내용을 바탕으로 번역과 요약을 하였다. 우선, 그래프 구조의 데이터가 무엇인지, 왜 사용하는 지 알아보려고 한다.
그래프 이론
그래프란 노드(아래 그림의 원)들이 다양한 연결관계를 갖고 있는 자료 구조이다. 아래 그림의 원으로 표시된 노드(nodes)와 선 엣지(edges)로 이루어져 있다. 노드를 vertices라고도 한다. 그래프는 수학적으로 개체 간의 관계를 나타내는데 쓰이며 G = (V, E)와 같이 정의된다. V는 노드의 집합, E는 엣지이다.
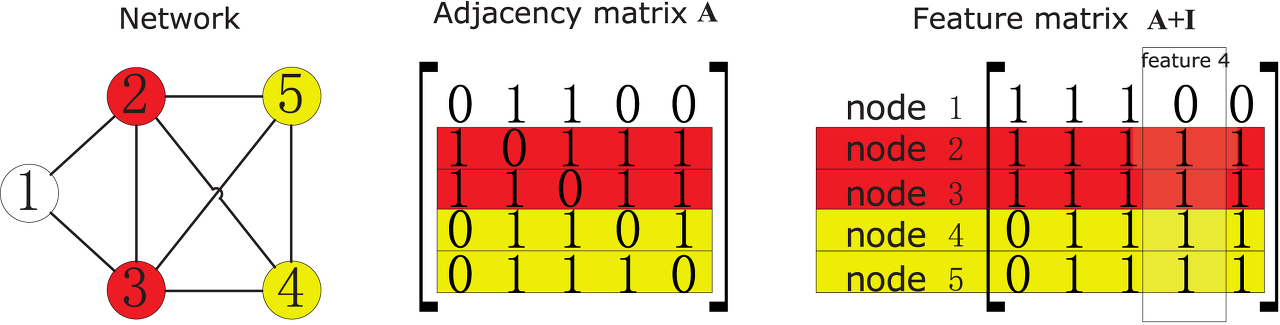
그래프를 왼쪽 그림과 같이 네트워크로 표현할 수도 있지만, 인접행렬(Adjacency matrix)로도 표현가능하다. 그래프가 N개의 노드를 가지고 있다면, (N x N)의 행렬로 나타낼 수 있다. 행렬의 원소는 두 노드 간 간선(엣지)이 있으면 1 없으면 0이다. 대각 행렬을 기준으로 대칭이라는 특징이 있다.
feature matrix는 왜 만들까? 빨간색으로 표시한 2, 3번 노드는 자신을 제외한 모든 노드와 연결되어있다. 노란색으로 표시된 4, 5번 노드는 1번을 제외한 모든 노드와 연결되어 있다. 자기 자신을 제외한 다른 노드들 간의 관계를 보면 빨간색과 노란색은 같은 집합으로 묶을 수 있다. 하지만, 인접행렬로 나타내면 두 집합의 원소가 다르다. 빨간색은 [1 0 1 1 1], [1 1 0 1 1]이다. 여기에 단위 행렬 I를 더해주면 2번 노드의 특징 행렬(feature matrix)는 [1 1 1 1 1]이로 3번 노드도 [1 1 1 1 1]로 같아진다.
정리하자면, 2번과 3번은 자기 자신을 제외한 모든 노드와 연결되어 있다는 점에서 같은데 이를 나타내기 위한 방법이 feature matrix를 만드는 것이다.
그래프 구조는 왜 분석하기가 어려울까?
우선, 그래프는 유클리디안 공간에 있다고 말할 수 없다. 즉, 우리가 사용하는 좌표계로 나타낼 수 없다는 말과 같다. 이런 특징 때문에 그래프 구조를 해석하는 것은 이미지나 시계열 데이터와 같은 데이터를 해석하는 것보다 훨씬 어렵다.
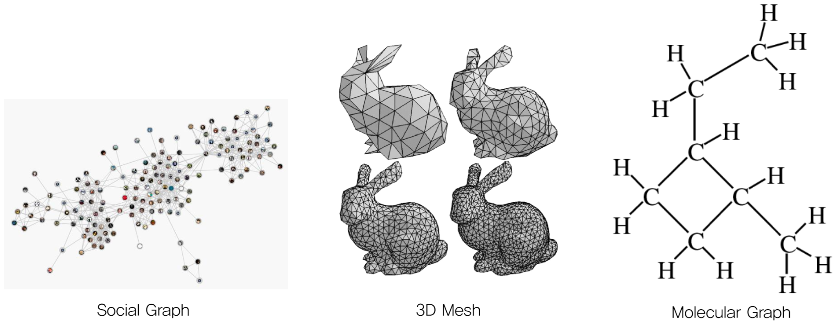
분자 구조나 토끼의 형태를 2차원과 3차원으로 나타낼 수는 있지만 기존의 좌표계로 나타내기는 매우 어렵다.
두 번째로, 그래프는 고정된 형태를 가지고 있지 않을 수 있다. Social 그래프의 예시를 보면 관계만 동일하다면 네트워크 구조로 표현하는 방법은 무수히 많다. 각 노드에 번호가 있다면 인접행렬은 하나겠지만, 아니라면 회전, 대칭에 의해 다른 인접행렬이 나올 수 있다. 만약, 인접행렬이 같으면 두 그래프를 같다고 말할 수 있을까? 아마 아닐 것이다. 분자의 경우 위 예시처럼 분자 구조를 표현한다고 해도 실제 3차원 공간 상에서는 1가지 이상의 경우가 나올 수 있다. 관계만 봐도 안되고 구조만 봐도 안되고.. 어려운 문제다..
왜 그래프를 사용할까?
1. 그래프는 관계나 상호관계와 같은 추상적인 개념을 구조화 하여 다루기에 좋다. 또한, 시각적으로 나타낼 수도 있다.
2. 복잡한 관계나 구조를 단순한 형태로 바꿨을 때 쉽게 문제가 해결되기도한다.
3. 사회적 관계 모델이나 사기 패턴, 에너지 소비 패턴 등 그래프 이론에 기반한 연구가 이미 되어있다.
전통적인 그래프 분석(탐색) 기법
1. 탐색 알고리즘 : BFS, DFS 등
2. 최단 경로 알고리즘 : 다익스트라 알고리즘, 최근접 이웃 등
3. spanning-tree 알고리즘: Prim's algorithm 등
4. 클러스터링 기법: k-means 등
Graph Neural Network(GNN)
GNN은 그래프 형태의 데이터에 바로 적용 가능한 신경망이다. GNN은 노드 레벨, 엣지 레벨, 그래프 레벨의 예측이 가능하다. 대표적으로 아래와 같은 neural network 들이 있다.
1. Recurrent Graph Neural Network
2. Spatial Convolutional Network
3. Spectral Convolutional Network
이어서 위의 neural network 들에 대해 알아보겠다.
'Statictics & Math & Data Science > Neural Networks' 카테고리의 다른 글
| [EfficientDet] 논문 리뷰: 가볍지만 성능은 좋은 object detector (0) | 2020.04.09 |
|---|---|
| [EfficientNet] 논문 리뷰: 모델의 파라미터(스케일링)에 대한 고찰 (0) | 2020.04.09 |
[SimPy] 파이썬 시뮬레이션: 기초 알아보기
[SimPy] 파이썬 시뮬레이션: 기초 알아보기
1. Environment
Environment 클래스를 객체화(선언)하는 것은 새로운 게임을 생성하는 것과 같다.
import simpy
env = simpy.Environment()
위와 같이 simpy의 Environment 클래스를 인스턴스화 하여 environment를 정의한다.
2. Process Interaction
Process는 다른 프로세스를 기다리거나 중간에 interrupt를 걸 수 있게 하는 env의 기능이다.
import simpy
env = simpy.Environment()
car = Car(env)
env.run(until=15)이 차는 전기차여서 충전시간이 필요하다. 충전은 charge()라는 함수로 구현하고 '5'라는 충전시간이 지나면 차는 출발한다.
class Car(object):
def __init__(self, env):
self.env = env
self.action = env.process(self.run())
def run(self):
charge_duration = 5
yield self.env.timeout(self.charge(charge_duration))
def charge(self, duration):
yield self.env.timeout(duration)운전자가 충전을 다 기다리지 않고 출발을 원한다면 어떻게 구현해야 할까? 충전은 run() 함수 안에서 돌아가므로, run()에 interrupt를 거는 함수를 만들 필요가 있다.
2-1 Interrupting another process
interrupting을 구현하기 위해 driver라는 함수를 만들었다.
def driver(env, car):
yield env.timeout(3)
car.action.interrupt()
이 함수는 클래스 내부에서 선언하지 않았다. 이 함수는 car라는 클래스 인스턴스를 파라미터로 받아 env.process를 interrupt 한다.
import simpy
env = simpy.Environment()
car = Car(env)
env.process(driver(env, car))
env.run(until=15)
3. Resources
리소스란 사용 가능한 자원이다. 예를 들어, 충전기가 5개인 충전소에 여러대의 차들이 충전을 하러 오는 상황을 생각해 볼 수 있다. 그리고 일반적인 카페와 같이 만들어서 파는 생산자-소비자 관계가 있을 수 있다.
def car(env, name, station, driving_time, charge_duration):
yield env.timeout(driving_time) # 차가 돌아다니다가 들어올 시간
print(f'{name} 차가 충전소에 {env.now}에 도착했습니다.)
with station.request() as req:
yield req
print(f'{name} 차가 충전을 시작한 시간 {env.now}')
yield env.timeout(charge_duration)
print(f'{name} 차의 충전이 완료된 시간 {env.now}')
import simpy
env = simpy.Environment()
station = simpy.Resource(env, capacity=2)
for i in range(4):
env.process(car(env, f'Car {i}', station, i*2, 5))
env.run()
Resource클래스를 station으로 인스턴스화했고 Resource 인스턴스는 request() 함수를 사용할 수 있다. 이 함수는 리소스인 station이 다시 사용가능해질 때까지 기다리게 한다. station의 리소스 총량은 capacity 값으로 정할 수 있다.
여기서 충전소가 차에게 리소스를 제공하는 형태는 FIFO(first in first out) 방식이다.
'Computer Science > Python' 카테고리의 다른 글
| [Python] Unable to create process using~(Flask, Locust etc.) (0) | 2022.04.07 |
|---|---|
| [sklearn] cython 코드 수정하기 (0) | 2020.08.27 |
| [python] pip install - urlopen error [SSL: CERTIFICATE_VERIFY_FAILED] (0) | 2017.11.29 |
| [Tensorflow] 텐서플로우 자료형 (0) | 2017.06.03 |
| [Python] Virtualenv 가상환경 구성하기 (0) | 2017.05.31 |
Contrast set learning & treatment learning (STUCCO, TAR3)
1. Contrast set learning
Before starting: contrast set은 대조군이라는 말과 같으며, 대조할 수 있도록 데이터 내에서 여러가지 다른 속성을 가지는 경우를 말한다. contrast set은 속성-값 쌍 형태로 이루어져 있다.

Contrast set learning은 연관 규칙 학습의 형태로, 각 그룹을 잘 구분할 수 있는 주요 predictors를 찾는 학습 방법이다. 연관 규칙 모델은 일반적으로 training set에서 일반적으로 함께 발생하는 속성을 연결하는 규칙을 제공한다. 예를 들어, 4년 짜리 프로그램에 등록하고 전체 과정을 수료한 사람들은 캠퍼스 근처에 사는 경향이 있다. 대조군 학습자는 현재 상황을 설명하는 규칙을 찾는 대신 그룹 간 분포에서 의미가 다른 규칙을 찾는다. 따라서, 이러한 그룹의 예측 변수로 사용할 수 있다. 예를 들어 contrast set learner는 "학사 학위 소지자나 박사 학위 소지자의 주요 식별자는 무엇이며, 박사 학위 소지자는 어떻게 다른가?"라고 질문할 수 있다.
데이터 마이닝은 일반적으로 개체의 특성을 분류하고 관찰된 항목이 어떤 범주에 속하는지 예측하는 것이다. 이 과정에서 학습 데이터를 이용하고, 새로운 데이터가 입력된다면 추가적으로 학습함으로써 기존의 가설(모델)을 개선한다. 반면, Contrast set learning의 학습방식은 이와는 반대이다. 학습된 분류 모델은 새로운 데이터를 각 클래스로 나누누는 반면, contrast set learning은 항목이 속한 범주를 이용하여 데이터가 특정 클래스로 판정되는 통계적 증거를 거꾸로 찾아낸다. 즉, contrast set 모델은 속성 값을 클래스 분포의 변경과 연관되는 규칙을 찾는다. 즉, 한 분류와 다른 분류를 대조하여 주요 예측 변수를 식별하려고 한다.
예를 들어, 항공 우주 공학자는 새로운 로켓의 시험 발사에 대한 데이터를 기록할 것이다. 로켓의 궤적, 작동 온도, 외부 압력 등과 같은 요인은 발사 내내 주기적으로 측정될 것이다. 로켓 발사가 여러 번의 성공적인 시험 후에 실패한다면, 엔지니어는 대조군 집합 학습을 사용하여 성공과 실패의 시험을 구별할 수 있다. 이러한 데이터를 학습시켜 contrast set learning을 적용하면, 각 시험의 주요 예측 변수 대 성공한 시험의 핵심 예측 변수(온도가 너무 높았고 풍압이 너무 높았던 경우 등)를 나타내는 일련의 연관 규칙을 생성한다. 이처럼 어떤 constrast set이 예측 변수를 다르게 만들었는지 찾는 것이 문제이다.
C4.5와 같은 표준 분류 알고리즘은 클래스의 중요성에 대한 개념이 없다(즉, 클래스가 "좋은" 것인지 "나쁜" 것인지 알지 못한다). 이러한 모델들은 원하는 클래스로 예측되도록 bias를 주거나 필터링할 수 없다. Contrast set learning의 목표는 그룹 간의 의미 있는 차이를 발견하는 것이므로, 특정한 클래스로 분류되도록 목적을 가지고 모델을 학습시키는 것이 좋다. MINWAL 또는 TAR 알고리즘과 같은 contrast set learner는 각 클래스에 가중치를 부여하는 방식을 사용한다.
Example: Supermarket Purchases
분류, 연관 규칙 학습, contrast set learning의 차이점은 간단한 슈퍼마켓 예시로 설명할 수 있다. 다음의 작은 데이터 집합에서 각 행은 슈퍼마켓 거래로, 각 "1"은 해당 품목이 구매되었음을 나타내며, 0"은 해당 품목이 구매되지 않았음을 나타낸다.
| Hamburger | Potatoes | Foie Gras | Onions | Champagne | 구입 목적 |
| 1 | 1 | 0 | 1 | 0 | 요리 |
| 1 | 1 | 0 | 1 | 0 | 요리 |
| 0 | 0 | 1 | 0 | 1 | 기념일 |
| 1 | 1 | 0 | 1 | 0 | 요리 |
| 1 | 1 | 0 | 0 | 1 | 파티 |
- 연관 규칙 학습은 양파와 감자를 함께 사는 고객들도 햄버거 고기를 살 가능성이 높다는 것을 발견할 수 있다.
- 분류에 따르면 양파, 감자, 햄버거 고기를 산 고객들은 요리할 물건을 구입하고 있었다는 것을 발견할 수 있다.
- Contrast set learning은 요리를 하려는 고객과 기념일 저녁 식사를 위한 쇼핑 간의 주요한 차이점을 발견한다. 요리를 하려는 고객들은 양파와 감자, 햄버거 고기를 구입하고 그리고 푸아그라나 샴페인은 사지 않는다.
변수가 많아지면 탐색 공간이 속성-값 쌍의 수에 지수적으로 증가하여 매우 커지므로 쉽게 탐색할 수 없다.
※ 연관 규칙과 Support
연관 규칙에서 규칙의 효용성을 나타내는 지표는 지지도(support)와 신뢰도(confidence), 향상도(lift)가 있다. 그 중 지지도는 조건부 확률에서 조건이 일어날 확률로 정의된다.
$${\displaystyle \mathrm {supp} (X)={\frac {|\{t\in T;X\subseteq t\}|}{|T|}}} $$
아래의 표를 이용하여 지지도 X ={beer, diapers} 의 지지도를 구해보면 1/5=0.2 이다.

$${\mathrm {lift}}(X\Rightarrow Y)={\frac {{\mathrm {supp}}(X\cup Y)}{{\mathrm {supp}}(X)\times {\mathrm {supp}}(Y)}}$$
이를 이용하여 \( \textrm{{milk, bread}} \Rightarrow \textrm{{butter}} \) 를 계산하면 $$ \frac{0.2}{0.4\times 0.4}=1.25 $$
2. Treatment learning
Treatment learning은 하나의 '원하는' 그룹을 취하여 나머지 '원하지 않는' 그룹과 대조되도록 하는 weighted contrast-set learning의 한 형태이다(desirability 수준은 weighted class로 표현된다). Treatment learning의 결과는, 적용되었을 때 원하는 출력을 이끌어내는 일련의 규칙을 제시한다.
Treatment learning은 contrast-set learning과 달리 다음과 같은 제약조건을 가진다.
- Treatment learning은 모든 그룹 간의 차이를 추구하기 보다는 초점을 맞출 특정 그룹을 지정하고, 이 원하는 그룹에 가중치를 적용하며, 나머지 그룹을 하나의 "원하지 않는" 범주로 묶는다.
- Treatment learning은 최소 이론에 명시적으로 초점을 맞추고 있다. 실제로 treatment는 최대 4가지 제약조건으로 제한된다. 즉, 로켓이 스케이트보드와 다른 이유를 모두 진술하는 것이 아니라, treatment learner는 로켓으로 예측할 때 높은 통계적 유의도를 가지는 1~4가지 주요 차이점을 제시한다.
단순함은 treatment learner가 추구하는 중요한 목표이다. Treatment learning은 클래스 분포에 가장 큰 영향을 미치는 가장 작은 변화에 주목한다.
treatment learning은 모든 속성이 가지는 값 범위의 모든 가능한 부분 집합을 탐색한다. 그러한 탐색은 실제로 실행될 수 없는 경우가 많기 때문에 treatment learning은 속성 범위를 빠르게 가지치기 하고 무시한다. 하지만, 이러한 방식 적용하면 원하는 클래스가 소수인 계층이 있는 계층 분포를 초래한다.
Example: Boston housing data
다음은 보스턴시의 주택 데이터에 대한 treatment learner TAR3의 출력의 예제이다. 이 데이터 셋에서는 각 주택에 대해 여러 가지 요인을 수집하고, 각 주택은 low, medium-low, medium-high, high로 분류한다. '원하는' 클래스는 "높음"으로 설정되며, 다른 클래스는 '원하지 않는' 클래스로 일괄 처리된다.
TAR3의 출력은 다음과 같다.
Baseline class distribution:
low: 29%
medlow: 29%
medhigh: 21%
high: 21%
Suggested Treatment: [PTRATIO=[12.6..16), RM=[6.7..9.78)]
New class distribution:
low: 0%
medlow: 0%
medhigh: 3%
high: 97%적용된 treatment(규칙)가 없는 경우 원하는 클래스는 전체 클래스 분포의 21%에 불과하다. 그러나 6.7~9.78개의 방과 이웃이 학부모-교사의 관계를 가지는 비율이 12.6~16인 비율을 가진 주택으로 데이터 셋을 필터링하면 97%가 원하는 등급(높은 등급의 주택)으로 분류된다.
3. 알고리즘
여러 Contrast set learning 알고리즘 중에 STUCCO와 TAR3에 대해 알아보자.
STUCCO
STUCCO는 contrast set을 학습하는데 트리 탐색 문제로 접근한다. 루트 노드는 빈 대조군이며, Children은 (동일한 노드를 두 번 방문하는 것을 피하기 위해) 표준적인 속성 순서를 통해 선택된 추가 아이템으로 세트를 전문화하여 추가된다. 아이들은 주어진 순서에 따라 기존의 모든 용어를 추가함으로써 형성된다. 형성된 나무는 너비 우선으로 탐색된다. 각 레벨의 노드를 고려하여 데이터 세트를 스캔하고 각 그룹에 대해 support을 계산한다. 그런 다음 각 노드를 검사하여 중요하고 큰지 여부, 잘라내야 하는지 여부 및 새 아이를 생성해야 하는지 여부를 판단한다. 모든 유의한 대조군을 배치한 후, 포스트 프로세서는 사용자에게 보여줄 서브셋을 선택한다. 즉, 낮은 순서, 단순한 결과가 먼저 표시되고, 그 다음에 "의미가 있는" 상위 순서 결과가 나타난다.[3]"
지원 계산은 대조군 집합 지원이 모든 그룹에서 동일하다는 귀무 가설(즉, 대조군 집합 지원은 그룹 구성원 자격과 무관함)을 시험하는 데서 나온다. 각 그룹에 대한 지원 카운트는 각 행이 대조군의 진가를 나타내고 각 열 변수가 그룹 멤버쉽 주파수를 나타내는 우발상황표에서 분석할 수 있는 주파수 값이다. 대조 세트 주파수와 귀무 가설의 비율 차이가 있는 경우, 알고리즘은 비율의 차이가 변수 사이의 관계를 나타내는지 또는 무작위 원인에 기인할 수 있는지를 결정해야 한다. 이는 관측된 주파수 카운트를 예상 카운트와 비교하는 카이-제곱 검정을 통해 결정할 수 있다.
노드의 모든 분기가 유의미하고 조건 절이 더 이상 많아질 수 없을 때 노드는 트리에서 제거된다. Pruning 방법은 다음과 같다.
최소 편차 크기: 두 그룹의 support 간의 최대 차이는 사용자가 지정한 임계값보다 커야 한다. 즉, 대비하고자 하는 그룹의 support 간 차이가 적으면 조건에 따라 구분이 안될 가능성이 높다.
기대 샘플의 비율: 결과를 잘 구분하는 조건(contrast set)이 구체화됨에 따라 결과 테이블에서 기대하는 샘플(조건에 맞는 샘플)의 빈도(confidence)가 감소할 수 있다. 이러한 빈도가 너무 작을 경우 카이-제곱 검정의 유효성을 위반한다.
\( {\displaystyle \chi ^2} \) 경계: 귀무 가설이 참일 때 계산된 통계의 분포에 상한선이 유지된다. 노드는 더 이상 이 컷오프를 충족시킬 수 없을 때 제거된다.
TAR3
TAR3 weighted contrast set learner는 규칙 집합의 lift(향상도)와 support(지지도) 두 가지 기본 개념을 기반으로 한다.
규칙 집합에서 lift란 조건과 결과가 서로 독립일 때와 비교해 두 사건이 동시에 얼마나 발생하는지를 나타내는 지표이다. 쉽게 말해 엑셀에서 어떤 컬럼에 조건 필터를 적용했을때, 우리가 보고자 하는 결과가 전체에서 차지하는 비율이 같으면 lift가 1이다.
lift가 1이면 \( P(A\cap B)=P(A)\cdot P(B) \)가 되어 A와 B가 독립임을 뜻한다. 따라서 규칙 사이에 유의미한 연관성이 없다는 뜻이다. 만약 lift가 2이면 필터를 적용했을 때 우리가 찾는 결과(예를 들어 y가 20~25 인 row)가 필터를 적용하기 전보다 2배 많아졌다는 뜻이다. 즉, 필터 조건(조건절)이 매우 유효하다고 할 수 있다. 어떤 결정(조건 적용)이 그 결정을 내린 후 샘플의 변화(즉, 규칙의 부과에 대응하여 클래스의 분포가 어떻게 변화하는지)에 따라 lift가 달라진다.
$$ lift(A\rightarrow B)\frac{P(A,B)}{P(A)\cdot P(B)} $$
TAR3은 각 클래스의 빈도에 따라 가중치를 부과한다. 그리고 규칙 셋은 최소화하고 클래스의 변화가 가장 크도록하는 규칙을 찾는다. 향상도(lift)를 계산할 때, 규칙이 적용되지 않은 베이스라인 스코어를 기준으로 하여 규칙이 적용됐을 때의 값을 베이스라인 스코어로 나눈다. Lift score의 역함수를 적용함으로써, TAR3 학습자는 기존 클래스는 선택하고 타겟 클래스는 reject 한다.
규칙 집합의 lift만 보고 유효성을 판단하는 것은 문제가 있다. 잘못된 데이터나 노이즈가 있을 경우 지지도(lift) 값은 높지만 규칙의 오버피팅을 유발할 수 있다. 오버핏된 규칙은 lift 값이 클 수 있지만 데이터 셋 내의 현재 상태를 정확하게 반영하지 못한다. 오버핏을 피하기 위해 TAR3는 support의 임계값을 활용한다. 즉, 조건절을 적용했을 때, 조건에 맞는 샘플이 너무 적으면 통계적 유의미성을 잃는다고 판단하는 것이다. 타겟 클래스가 주어졌을 때의 support 임계값은 사용자 지정 값(일반적으로 0.2)으로, 전체 데이터 셍에서 target 클래스의 비율과 규칙 집합이 적용되었을 때의 대상 클래스의 비율을 비교한다. TAR3은 이 임계값보다 낮은 support를 가진 모든 규칙 집합을 reject한다.
높은 lift와 높은 support 값을 모두 요구함으로써 TAR3는 이상적인 규칙 집합을 반환할 뿐만 아니라 낮은 복잡도의 규칙 집합을 만들도록 한다.
TAR3 알고리즘은 높은 heuristic 값을 가진 속성 값 범위에서만 규칙 집합을 만든다. 이 알고리즘은 lift score를 결정할 때, 각 속성 값의 범위를 고려한다. 그리고 각 속성 별 스코어를 정렬한 후 누적 누적 확률 분포로 변환된다. TAR3는 이 분포에서 무작위로 값을 선택하는데, 이는 낮은 점수 범위를 선택할 가능성이 낮다는 것을 의미한다. 또한, 높은 점수 범위를 선택할 가능성도 낮아지는데 이는 규칙의 과적합을 방지할 수도 있다. 후보 규칙 집합을 생성하기 위해 몇 몇 범위를 선택하고 결합한다. 그런 다음 이 후보 규칙 집합을 채점하고 분류한다. 사용자가 정의한 라운드 횟수 후에도 개선이 보이지 않으면 알고리즘이 종료되어 최상위 점수 규칙 집합을 반환한다.
Reference
'Statictics & Math & Data Science' 카테고리의 다른 글
| [엑셀 데이터 분석] 상관분석(Correlation) (2) | 2017.05.21 |
|---|
[LightGBM] LGBM는 어떻게 사용할까? (설치,파라미터튜닝)
[LightGBM] LGBM는 어떻게 사용할까?
1. Light GBM이란?
Light GBM은 트리 기반의 학습 알고리즘인 gradient boosting 방식의 프레임 워크이다.
2. 다른 트리 기반의 알고리즘과 무엇이 다른가?
Light GBM은 나무를 수직으로 확장한다. 반면 다른 알고리즘은 나무를 수평으로 확장한다. 따라서 기존의 알고리즘은 수평으로 확장하여 포화 트리를 만드는 방향으로 학습하는 반면 leaf-wise tree growth인 LGBM은 최대 delta loss가 증가하도록 잎의 개수를 정한다. leaf-wise알고리즘은 다른 level-wise 알고리즘보다 낮은 loss를 달성하는 경향이 있다. 데이터의 크기가 작은 경우 leaf-wise는 과적합(overfitting)되기 쉬우므로 max_depth를 줄여줘야 한다.
3. LGBM은 왜 이렇게 유명해졌나?
데이터의 크기가 커짐에 따라 빠른 결과를 내는 것도 중요해지고 있다. 그런점에서 Light GBM은 'Light'의 접두사와 같이 속도가 빠른 것이 장점이다. 메모리를 적게 차지하고 속도가 빠르다는 장점 외에도, LGBM은 결과의 정확도가 높다는 장점이 있다. 또한, GPU를 활용할 수 있기 때문에 널리 사용되고 있다.
하지만, 위에서 말했듯이 overfitting에 민감하여 데이터의 크기가 작을 경우 기존의 머신러닝 알고리즘이 더 좋을 수 있다. 경험적으로 데이터의 개수(행 수)가 10,000개 이상일 때 추천한다.
4. 설치하기
conda install -c conda-forge lightgbm
pip install lightgbmSample code
import lightgbm as lgb
train_ds = lgb.Dataset(X_train, label = y_train)
test_ds = lgb.Dataset(X_val, label = y_val)
params = {'learning_rate': 0.01,
'max_depth': 16,
'boosting': 'gbdt',
'objective': 'regression',
'metric': 'mse',
'is_training_metric': True,
'num_leaves': 144,
'feature_fraction': 0.9,
'bagging_fraction': 0.7,
'bagging_freq': 5,
'seed':2020}
model = lgb.train(params, train_ds, 1000, test_ds, verbose_eval=100, early_stopping_rounds=100)
y_pred=model.predict(X_val)위의 예제는 회귀 모델을 만들기 위한 예제 코드이다. 분류 모델을 만들기 위해서는 아래와 같이 바꾸면 된다.
- objective를 ‘binary’로 지정
- metric을 ‘binary_logloss’로 지정
5. 하이퍼파라미터
주요 파라미터
object
objective 🔗︎, options: regression, binary, multiclass...metric
metric 🔗︎, options: mae, rmse, mape, binary_logloss, auc, cross_entropy, kullbac_leibler...1. learning_rate
일반적으로 0.01 ~ 0.1 정도로 맞추고 다른 파라미터를 튜닝한다. 나중에 성능을 더 높일 때 learning rate를 더 줄인다.
2. num_iterations
기본값이 100인데 1000정도는 해주는게 좋다. 너무 크게하면 과적합이 발생할 수 있다.
같은 뜻으로 사용되는 옵션: num_iteration, n_iter, num_tree, num_trees, num_round, num_rounds, num_boost_round, n_estimators
3. max_depth
-1로 설정하면 제한없이 분기한다. feature가 많다면 크게 설정한다. 파라미터 설정 시 우선적으로 설정한다.
4. boosting
부스팅 방법: 기본값은 gbdt이며 정확도가 중요할때는 딥러닝의 드랍아웃과 같은 dart를 사용한다. 샘플링을 이용하는 goss도 있다.
boosting 🔗︎, default = gbdt, options: gbdt, rf, dart, goss
gbdt : traditional Gradient Boosting Decision Tree, aliases: gbrt
rf : Random Forest, aliases: random_forest
dart : Dropouts meet Multiple Additive Regression Trees
goss : Gradient-based One-Side Sampling
5. bagging_fraction
배깅을 하기위해서 데이터를 랜덤 샘플링하여 학습에 사용한다. 비율은 0 < fraction <= 1 이며 0이 되지 않게 해야한다.
6. feature_fraction
feature_fraction이 1보다 작다면 LGBM은 매 iteration(tree)마다 다른 feature를 랜덤하게 추출하여 학습하게된다. 만약, 0.8로 값을 설정하면 매 tree를 구성할 때, feature의 80%만 랜덤하게 선택한다. 과적합을 방지하기 위해 사용할 수 있으며 학습 속도가 향상된다.
7. scale_pos_weight
클래스 불균형의 데이터 셋에서 weight를 주는 방식으로 positive를 증가시킨다. 기본값은 1이며 불균형의 정도에 따라 조절한다.
8. early_stopping_round
Validation 셋에서 평가지표가 더 이상 향상되지 않으면 학습을 정지한다. 평가지표의 향상이 n round 이상 지속되면 학습을 정지한다.
9. lambda_l1, lambda_l2
정규화를 통해 과적합을 방지할 수 있지만, 정확도를 저하시킬수도 있기 때문에 일반적으로 default 값인 0으로 둔다.
- 더 빠른 속도
- bagging_fraction
- max_bin은 작게
- save_binary를 쓰면 데이터 로딩속도가 빨라짐
- parallel learning 사용
- 더 높은 정확도
- max_bin을 크게
- num_iterations 는 크게하고 learning_rate는 작게
- num_leaves를 크게(과적합의 원인이 될 수 있음)
- boosting 알고리즘 'dart' 사용
- 과적합을 줄이기
- max_bin을 작게
- num_leaves를 작게
- min_data_in_leaf와 min_sum_hessian_in_leaf 사용하기
[이미지 및 내용 출처]
1. https://lightgbm.readthedocs.io/en/latest/Features.html
'Statictics & Math & Data Science > 파이썬 데이터 분석' 카테고리의 다른 글
| [Pandas] read_csv 시 UnicodeDecode 에러 : utf-8 인코딩 문제 (0) | 2020.04.23 |
|---|---|
| [Regression] Ridge and Lasso Regression in Python (3) - Lasso (0) | 2019.01.31 |
| [Regression] Ridge and Lasso Regression in Python (2) - Ridge (0) | 2019.01.31 |
| [Regression] Ridge and Lasso Regression in Python (1) - Polynomial (0) | 2019.01.31 |
| [Regression] Piecewise Regression with numpy (0) | 2019.01.29 |
[Math] 범함수와 최적제어 변분법의 관계
[Math] 범함수와 최적제어 변분법의 관계
1. 범함수란?
범함수를 이해하기 위해 함수와 비교해 보자.
- 함수는 실수를 입력받아 실수를 출력한다.
- 범함수는 함수를 입력받아 실수를 출력한다.
예를 들어, 기대값을 계산할 때에는 확률분포함수를 입력으로 하여 실수를 출력한다.
범함수는 보통 대문자로 표기하며 도립변수인 함수를 대괄호로 감싼다.
ex) F[y(x)]
대부분의 범함수 값은 정적분으로 계산한다. 예를 들어, 확률변수 X의 기대값과 엔트로피는 확률밀도함수 p(x)를 적분한 값이다.
2. 최적제어와 변분법
범함수 F[y(x)]의 값을 최대화하거나 최소화하는 독립함수 y(x)를 찾는 것을 최적제어라고 한다.
변분법은 수학의 한 분야로, 범함수의 최소, 최대를 찾는 방법을 가리키는 용어이다.
변분법은 오일러로부터 시작해서 라그랑주가 발전시켰다. 이후 최적제어론과 동적계획법으로 계승되어 발전한다.
변분법의 한 예로 최단시간 강하곡선 문제가 있다. "이 문제는 직선이 최단거리는 되지만 최단시간은 아니다." 라는 것이다.
최단시간의 경로를 푸는 방법은 시간 = 거리/속도의 식에서 t를 적분하는 방식으로 유도해나가는 것이다.
문제의 정의에 따라 이 적분값을 최소가 되게 하는 곡선을 찾아야 한다.

정리:
함수에서는 어떤 함수 값의 최대/최소가 되는 x를 찾기위해 미분을 해서 극대, 극소점을 찾기도 하고 제한조건을 이용하여 찾기도한다. 반면 ,변분법의 개념에서는 어떤 범함수가 최대/최소가 되는 입력함수를 찾는 것이 목표이고, 다시말해 최적제어이다.




