그래프 구조를 가지는 데이터의 분석에 Graph Neural Network(GNN)이 언급되면서 관심을 받고 있다. 사실 그래프 이론자체가 쉽게 와닿는 내용이 아니고, 이해하기 위해 여러 자료도 봤지만 한 번에 이해를 하지 못했다. 그 중 Medium 의 블로그를 참고하여 이해한 내용을 바탕으로 번역과 요약을 하였다. 우선, 그래프 구조의 데이터가 무엇인지, 왜 사용하는 지 알아보려고 한다.
그래프 이론
그래프란 노드(아래 그림의 원)들이 다양한 연결관계를 갖고 있는 자료 구조이다. 아래 그림의 원으로 표시된 노드(nodes)와 선 엣지(edges)로 이루어져 있다. 노드를 vertices라고도 한다. 그래프는 수학적으로 개체 간의 관계를 나타내는데 쓰이며 G = (V, E)와 같이 정의된다. V는 노드의 집합, E는 엣지이다.
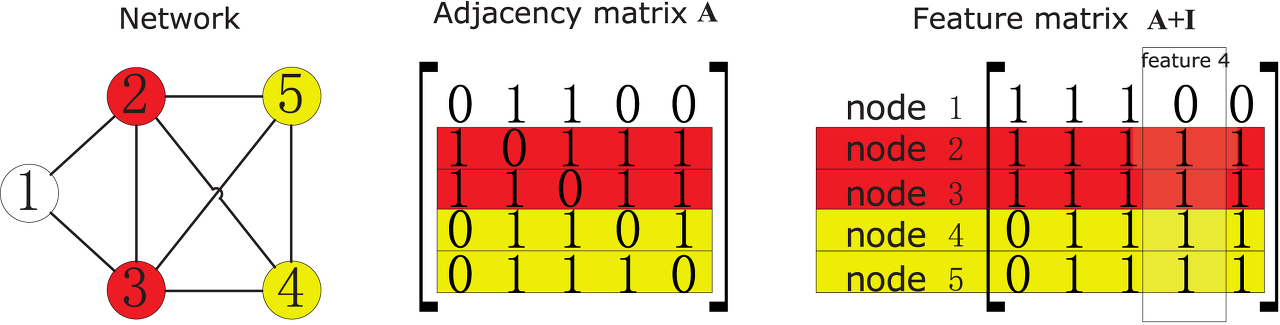
그래프를 왼쪽 그림과 같이 네트워크로 표현할 수도 있지만, 인접행렬(Adjacency matrix)로도 표현가능하다. 그래프가 N개의 노드를 가지고 있다면, (N x N)의 행렬로 나타낼 수 있다. 행렬의 원소는 두 노드 간 간선(엣지)이 있으면 1 없으면 0이다. 대각 행렬을 기준으로 대칭이라는 특징이 있다.
feature matrix는 왜 만들까? 빨간색으로 표시한 2, 3번 노드는 자신을 제외한 모든 노드와 연결되어있다. 노란색으로 표시된 4, 5번 노드는 1번을 제외한 모든 노드와 연결되어 있다. 자기 자신을 제외한 다른 노드들 간의 관계를 보면 빨간색과 노란색은 같은 집합으로 묶을 수 있다. 하지만, 인접행렬로 나타내면 두 집합의 원소가 다르다. 빨간색은 [1 0 1 1 1], [1 1 0 1 1]이다. 여기에 단위 행렬 I를 더해주면 2번 노드의 특징 행렬(feature matrix)는 [1 1 1 1 1]이로 3번 노드도 [1 1 1 1 1]로 같아진다.
정리하자면, 2번과 3번은 자기 자신을 제외한 모든 노드와 연결되어 있다는 점에서 같은데 이를 나타내기 위한 방법이 feature matrix를 만드는 것이다.
그래프 구조는 왜 분석하기가 어려울까?
우선, 그래프는 유클리디안 공간에 있다고 말할 수 없다. 즉, 우리가 사용하는 좌표계로 나타낼 수 없다는 말과 같다. 이런 특징 때문에 그래프 구조를 해석하는 것은 이미지나 시계열 데이터와 같은 데이터를 해석하는 것보다 훨씬 어렵다.
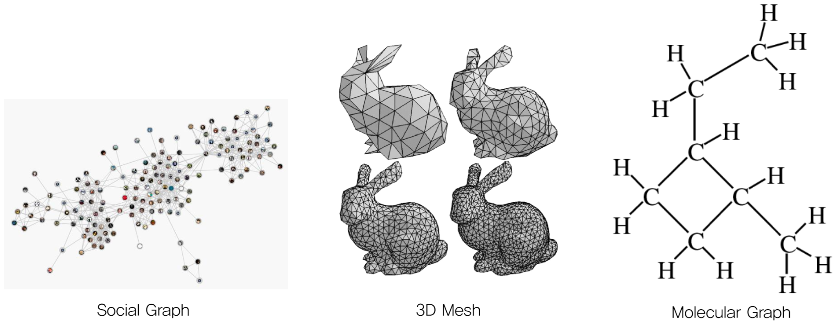
분자 구조나 토끼의 형태를 2차원과 3차원으로 나타낼 수는 있지만 기존의 좌표계로 나타내기는 매우 어렵다.
두 번째로, 그래프는 고정된 형태를 가지고 있지 않을 수 있다. Social 그래프의 예시를 보면 관계만 동일하다면 네트워크 구조로 표현하는 방법은 무수히 많다. 각 노드에 번호가 있다면 인접행렬은 하나겠지만, 아니라면 회전, 대칭에 의해 다른 인접행렬이 나올 수 있다. 만약, 인접행렬이 같으면 두 그래프를 같다고 말할 수 있을까? 아마 아닐 것이다. 분자의 경우 위 예시처럼 분자 구조를 표현한다고 해도 실제 3차원 공간 상에서는 1가지 이상의 경우가 나올 수 있다. 관계만 봐도 안되고 구조만 봐도 안되고.. 어려운 문제다..
왜 그래프를 사용할까?
1. 그래프는 관계나 상호관계와 같은 추상적인 개념을 구조화 하여 다루기에 좋다. 또한, 시각적으로 나타낼 수도 있다.
2. 복잡한 관계나 구조를 단순한 형태로 바꿨을 때 쉽게 문제가 해결되기도한다.
3. 사회적 관계 모델이나 사기 패턴, 에너지 소비 패턴 등 그래프 이론에 기반한 연구가 이미 되어있다.
전통적인 그래프 분석(탐색) 기법
1. 탐색 알고리즘 : BFS, DFS 등
2. 최단 경로 알고리즘 : 다익스트라 알고리즘, 최근접 이웃 등
3. spanning-tree 알고리즘: Prim's algorithm 등
4. 클러스터링 기법: k-means 등
Graph Neural Network(GNN)
GNN은 그래프 형태의 데이터에 바로 적용 가능한 신경망이다. GNN은 노드 레벨, 엣지 레벨, 그래프 레벨의 예측이 가능하다. 대표적으로 아래와 같은 neural network 들이 있다.
1. Recurrent Graph Neural Network
2. Spatial Convolutional Network
3. Spectral Convolutional Network
이어서 위의 neural network 들에 대해 알아보겠다.
'Statictics & Math & Data Science > Neural Networks' 카테고리의 다른 글
| [EfficientDet] 논문 리뷰: 가볍지만 성능은 좋은 object detector (0) | 2020.04.09 |
|---|---|
| [EfficientNet] 논문 리뷰: 모델의 파라미터(스케일링)에 대한 고찰 (0) | 2020.04.09 |