어떤 실험을 하고 결론을 내리기 위해선 가설 검정을 수행한 후 특정 통계량의 유의수준과 비교한다. 대게, p-value는 0.05나 0.01를 사용하곤 한다.
그러나 두 개 이상의 가설을 동시에 시험할 때(다중 비교) 통계적 추론이 잘못될 확률은 상당히 높아진다. False positive가 많이 발생하는데 생물학이나 의학에서는 이러한 거짓 양성(false positive)에 민감하여 p-value 조정(adjustment)이 필요하다. 하지만, 다양한 실험 특성에 적합한 adjustment 방법을 선택하기는 여전히 어렵다.
예를 들어 보자, Garcia-Arenzana(2014)은 스페인 여성들에게 유방암의 중요한 위험 요소인 유방조영술 밀도와 25가지 식이 변수의 연관성을 테스트했고 다음과 같은 결과를 확인했다.

보다시피 P<0.05를 만족하는 변수의 수는 5개이다. 하지만, 25개의 식이 변수를 동시에 검정했기 때문에, 식이요법이 유방조영학적 밀도에 실질적인 영향을 미치지 않았더라도, 한 두 개의 변수가 우연히 유의미한 결과를 보였을 거라고 예상했다. 이때, Bonferroni 보정을 적용하면 0.05를 25로 나눈 P<0.002를 만족해야된다. 그러면 총 칼로리(Total calories)만 유의하다.
아래에서 설명하겠지만 Bonferroni 보정의 사용은 일련의 검정에서 하나의 거짓 양성(false positive)가 문제가 될 때 적합하다. 하지만, 많은 변수를 한번에 검정해야 하고 그 중에서 의미있는 변수 여러 개를 찾고자 한다면, Bonferroni 보정은 거짓 음성(false negative)을 초래할 수 있다. 즉, 유의미한 변수를 놓칠 수 있다는 말이다.
예를 들어, 간암 조직과 정상 간 조직 사이에 있는 2만개의 유전자의 유의성을 비교한다고 하자. 당신은 의미가 서로 다른 다른 수십, 수백 개의 유전자를 찾기를 바라고 있다. 이때, Bonferroni 보정을 사용할 경우 P 값은 0.05/20000=0.0000025 보다 작아야 한다. 이렇게 되면, 단지, '단 하나의 거짓 양성도 포함하지 않는다'는 것을 확신하고자 한 이유만으로 많은 중요한 유전자 변수들을 놓칠 수 있다.
Bonferroni 교정의 중요한 문제는 통계 테스트의 "가족(family)"이 무엇인지 결정하는 것이다. 지금은 25개의 변수를 가지고 검정했는데, 여기에 연령, 교육, 사회적 지위 등과 같은 변수 13개가 추가된다면, P를 38로 나눠야 할까? 만약 이전 실험에서 다른 30개의 변수를 사용한다면 family를 55개로 정의해야 할까? 이처럼 Bonferroni adjustment에서는 family의 수를 정의하는데 어려움이 있다.
여기서 family-wise type 1 error의 개념이 나온다. family-wise type 1 error (FWER)란 family에서 false positive가 1개라도 발생할 확률을 의미한다.
FWER = 1 - Pr(V=0) = Pr(V>=1)
다중 비교 문제에 대한 고전적인 접근법은 이 FWER을 조절하는 것이다. 만약 FWER 이 0.05라면 한 연구에서 적어도 1개의 잘못된 결론이 나올 확률이 0.05라는 뜻이다. 이 FWER를 통제하기 위해 유의성 또는 알파에 대한 유의수준을 0.05로 설정하는 대신 더 낮은 임계값을 사용하는 방법이 있다.
1) Bonferroni adjustment
FWER 을 제어하는 가장 일반적인 방법은 Bonferroni 보정이다. Bonferroni adjustment는 FWER (일반적으로 0.05)을 검정 횟수로 나누어 개별 검정의 임계값(알파)을 찾는다. 만약, 100개의 통계적 시험을 수행하는 경우, 개별 검정의 임계값은 0.05/100=0.0005가 될 것이며, P<0.0005인 개별 검정은 유의하다고 간주한다.

하지만 Bonferroni 보정은 너무 보수적이어서 귀무가설이 잘 기각되지 않는 단점이 있다. 따라서 적절한 타협이 필요하다.
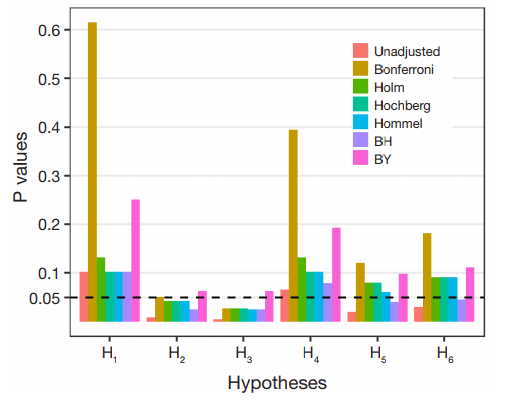
Multi-step 보정방법
2) Holm adjustment
Holm adjustment는 multi-step 방법 중 step-down에 해당 하는 방법이다. Bonferroni 기법을 기반으로하는 좀 덜 보수적인 방법이다. 이 방법은 가설의 유의성에 따라 정렬하는 방법을 사용하는데 그 방법은 아래와 같다.

p-value를 낮은 순으로 정렬하고 높은 rank 일수록 보수적으로 검정하는 방법이다.

3) Hochberg adjustment
Hochberg adjustment는 multi-step 방법 중 step-up에 해당 하는 방법이다. Holm method와 유사하게 Hochberg adjustment도 비슷한 방법을 사용한다.

하지만 Hochberg 방법은 p-value를 높은 순으로 정렬하고 \( p_{(i)} \leq \alpha^{'}_{(i)} \) 인 \( \textrm H_{(i)} \) 가 나오면 비교를 멈추고 유의 수준에서 귀무가설을 기각한다.
4) Hommel adjustment
Simes(1986)는 Bonferroni method를 수정하여 m개의 가설에 대해 global test를 하는 방법을 제안했다.
\( H=\{ H_{(1)}, ..., H_{(m)} \} \) 일 때, \( p_{(i)} \leq i\frac{\alpha}{m} \) 이면 귀무가설 H가 기각된다.하지만 Simes의 global test 는 개별적인 가설에 대해 접근하는 방법이 아니기 때문에 Hommel(1988)는 Simes의 방법을 확장하여 individual \( H_i \)에 대해 검정하는 방법을 제안한다.
$$ j=max \{ i \in \{ 1, ... , m \} : p_{(m-i+k)} > k{\alpha}/{i} \ for \ k=1, ... , i \}$$
만약 j 가 존재 하지 않는다면 모든 \( H_i \)는 기각되고, 존재한다면 \( H_i \)는 \( p_i \leq {\alpha}/{j} \) 를 만족하는 경우 기각한다.
5) Benjamini-Hochberg(BH) adjustment
FWER을 조절하는 방법과 달리 Benjamini와 Hochberg(1995)는 FDR(false discovery rate)을 조절하는 방법을 소개했다. FDR은 다중 비교에서 Type 1 error를 조절하는 또 다른 자주 쓰이는 지표로 유의하다고 판단한 가설 중 실제로 유의하지 않은 가설의 비율을 조절하는데 사용된다. FDR은 다음과 같이 정의한다.

여기서 m은 실험 횟수이고, \( m_0 \) 는 true(맞게 기각된) \( H_0 \) 의 수이다. R은 기각된 총 횟수, U는 잘못 기각된 \( H_0 \)의 수이다.

BH method는 아래의 방법으로 FDR 을 조절한다. q는 사전 정의된 FDR의 upper bound 이다. (e.g., q=0.05)
$$ k = max \{ i : p_{(i)} \leq \frac{i}{m}q \} $$
만약 k가 존재하지 않는다면 가설을 기각하지 못하고, 존재한다면 가설 \( H_i (i = 1, ... , k) \)를 기각한다. BH method는 p-value가 가장 큰 \( H_{(i)} \) (i=m, ..., 1) 부터 작은 순으로 비교 연산을 시작한다.
FDR 기반의 보정 방법은 다른 방법에 비해 덜 보수적이다. (Fig.1 참고) 그리고 실험 횟수가 많을 때 널리 사용된다.
아래의 그림을 보면, BH adjustment는 28개의 귀무가설을 기각하여, 보수적인 7개만 기각한 Holm's에 비해 어느정도 false positive를 허용한다.
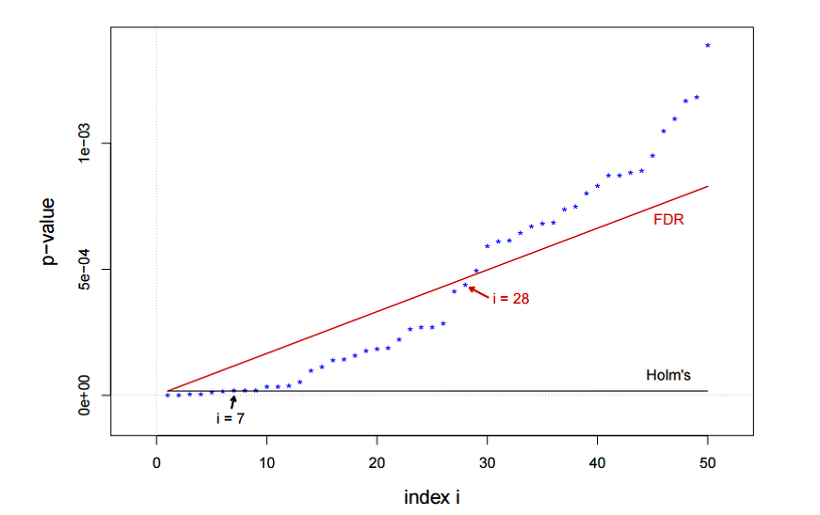
6) Benjamini-Yekutieli (BY) adjustment
BH method와 비슷하지만 좀더 보수적인 방법이다. 마찬가지로 FDR 을 사용하여 조절하는 방법이며 Benjamini과 Yekutieli(2001)이 제안했다. 마찬가지로 q는 사전 정의된 FDR의 upper bound이다.
BY method는 아래와 같이 계산된다.

k가 존재하지 않는다면 가설을 기각하지 않고, 존재하면 가설 \( H_i \)를 기각한다.
참조: Chen, S. Y., Feng, Z., & Yi, X. (2017). A general introduction to adjustment for multiple comparisons. Journal of thoracic disease, 9(6), 1725.
'Statictics & Math & Data Science > 통계&데이터분석' 카테고리의 다른 글
| [데이터분석] 매니폴드(manifold)란? (0) | 2019.04.03 |
|---|---|
| [통계] 차원의 저주와 K-NN(최근접이웃) 알고리즘 (0) | 2019.04.03 |
| [가중치 규제] L1 & L2 Regularization Method (0) | 2019.01.30 |
| [확률분포] 확률변수, 확률질량함수, 확률밀도함수 (0) | 2018.08.15 |
| [실험계획법] 분산 분석(1) 총변동의 분할 (0) | 2018.08.10 |