EfficientNet과 마찬가지로 EfficientDet은 모델 사이즈를 최소화하고 성능을 최대화하는 효율성에 초점을 맞춘 object detection 모델이다. 이 논문은 EfficientNet을 backbone 네트워크로 사용하였고 bi-directional feature pyramid network (BiFPN)을 이용하여 특징을 쉽고 빠르게 융합하는 방식을 제안하였다. 기존의 object detector는 region-of-interest proposal 단계를 가지는지 여부에 따라 two-stage 방식과 one-stage 방식으로 구분되었다. Two-stage detector가 더 정확하고 유연한 반면, one-stage detector는 사전에 정의된 anchor를 이용하여 간단하며 효과적인 방식으로 detection을 수행한다. Object detection에서 어려운 점 중에 하나는 상황에 따라 object의 크기가 달라지는 것을 고려해야 한다는 점이다. 따라서 멀티-스케일링 기법이 중요하며, feature pyramid network (FPN)을 시작으로 multi-scale feature를 합치는 방법이 연구되고 있다. M2det은 특징 합성을 위한 U-shape 모듈을 사용하였고, G-FRNet은 특징 정보를 컨트롤하기 위한 gate units을 도입하였다. 더 나은 성능을 얻기 위해, 베이스라인 detector의 스케일을 키우는 방식을 많이 사용하며 backbone 네트워크로 ResNet, ResNeXt, AmoebaNet을 사용하기도 한다.
아래의 그림은 EfficientDet의 전체적인 구조로, 전체적으로 one-stage detector의 패러다임을 따르고 있다. Backbone 네트워크인 EfficientNet의 level 3-7 features {P3, P4,P5,P6,P7} 를 추출하여 top-down과 bottom-up 양방향으로 특징 융합을 수행한다. 융합된 특징은 class/box 예측 네트워크로 전달되어 객체의 클래스와 바운딩 박스를 예측한다.

정확도와 효율성의 trade off를 최적화하는 baseline 모델을 선택하는 것은 매우 중요하다. 기존 연구는 ResNeXt와 AmoebaNet를 기반으로 큰 이미지를 대상으로 했다. 이러한 방법은 하나의 스케일링 차원에만 집중하기 때문에 효율적이지 못하다. 이러한 문제를 해결하기 위해. EfficientDet은 EfficientNet과 마찬가지로 효율적인 compound scaling 방식을 사용하였다. BiFPN을 구성할 때, 채널의 수는 지수적으로 증가시키고 레이어의 수는 선형적으로 증가시켰다.
Wbifpn=64∙1.35∅, Dbifpn=2+∅
Feature level이 3-7인 layer는 BiFPN이 사용되므로, 입력 이미지의 해상도를 27 로 나눠야 하며 해상도를 선형적으로 증가시키기위해 다음과 같음 방식으로 해상도를 결정하였다.
Rinput=512+∅∙128
Object의 location과 class를 예측하는 네트워크도 compound coefficient를 사용한다. 그 중 너비(width)는 BiFPN과 동일하고 (Wpred=Wbifpn ), 레이어 수는 다음과 같은 방식으로 결정한다.
Dbox=Dclass=3+∅∙128
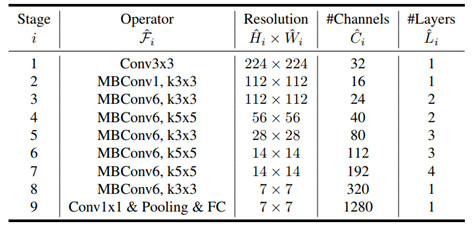
위의 식에서 compound coefficient ∅ 에 따라 EfficientDet-D0(∅=0 ) 부터 D6(∅=6) 까지 정리한 결과는 다음의 표와 같다.

아래의 표에서 #Params와 #FLOPS는 모델 파라미터와 연산의 수를 나타낸다. LAT는 배치 크기가 1일때의 의 추론 지연 시간을 나타내고, AA는 autoaugmentation 을 의미한다. EfficientDet은 mAP 성능이 유사한 object detection 모델과 비교하여 파라미터 수와 필요 연산량이 훨씬 적은 것을 확인할 수 있다. 따라서, 추론 속도도 동일 성능의 다른 모델에 비해 2배 가량 빠르다.

결론적으로, EfficientDet은 복합 스케일링 (compound scaling) 기법을 이용하여 효율적으로 성능을 향상시키고 #Params와 #FLOPS를 줄였다. Object detection 모델을 이용한 좌표 보정 알고리즘에서도 EfficientDet을 사용하여 부품의 위치와 레이블을 추론함으로써, 기존 detector 보다 정확도와 처리속도를 향상시킬 수 있었다.

[참조] TAN, Mingxing; PANG, Ruoming; LE, Quoc V, “Efficientdet: Scalable and efficient object detection.” arXiv preprint arXiv:1911.09070, 2019.
'Statictics & Math & Data Science > Neural Networks' 카테고리의 다른 글
| [EfficientNet] 논문 리뷰: 모델의 파라미터(스케일링)에 대한 고찰 (0) | 2020.04.09 |
|---|---|
| [GNN] (1) 데이터 구조 분석을 위한 Graph Neural Network(GNN) 소개 (0) | 2020.03.25 |